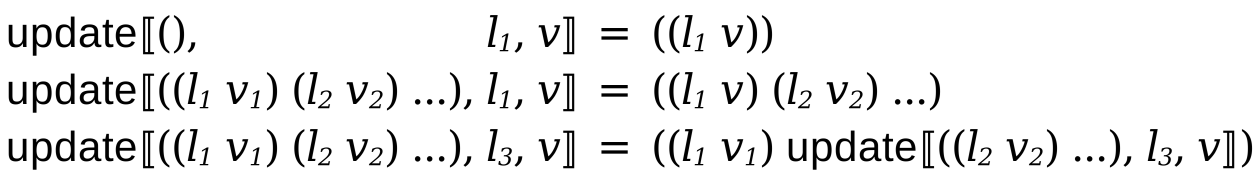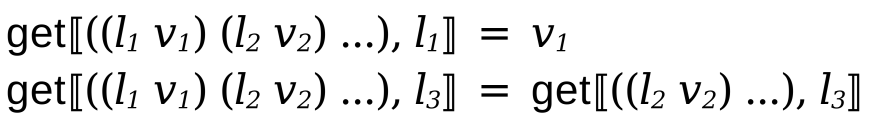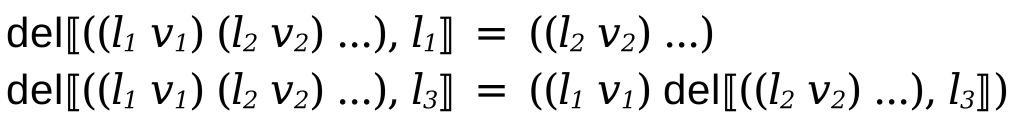12 Program State🔗

12.1 Imperative Languages🔗

Until this point in the class, we developed a pure functional programming language, i.e., you could create and pass functions around or apply them to other values. More importantly, all computations were expressed as function applications—arguments went in and the computed value was returned. This is a general model for expressing all kinds of computations, but it might still feel limiting. Many of you are used to imperative languages (like C or Python), where instead of function applications being nested, you are used to a sequence of statements that execute with the program. The goal of this module is to learn how to model such languages and understand how they work.

The key thing in these language is an implicit state. As the language executes individual statements, the statements compute a return value and/or modify this implicit state. Contrast this with our functional language where the only thing computed is the value returned, there is no state hidden away from the programmer like what happens in imperative languages. Through the following sections we will look at how we add state to our program.

We use state and store interchangeably.

12.2 Syntax🔗

First, we extend the surface syntax to write programs that have sequences of instructions. So we can write programs like below:

Here, the seq block describes a sequence of expressions to be evaluated. The result of the entire begin block is the result of the last statement, and all intermediate results are discarded. However, if all intermediate results are discarded there is no use of writing a sequence of statements! To access results of previous statements in a program, one needs to add to the language the ability to store and retrieve results of prior computations.

In its simplest form, storage is a place to put things so we can go back and get them. Storage can come in many forms - tape, disk, memory, USB sticks, firmware - but it always allows for values to persist in some form over time. Storage can be viewed abstractly as a collection of locations that are values for storing other values. Think of a location as a box and the value at a location as the contents of the box. The location is a value in the sense that it is constant and does not change, but the contents of a location can change. We dereference a location when we want the value it stores. Remember, a location is a value and as such can be calculated and returned without affecting the contained value. Dereferencing gets the value out and returns it.

Storage exists in the background and is there to use whenever needed. When we program we declare variables, pointers and references that all reference storage, but we don’t ever talk about storage as a whole unless we’re systems programmers. In C this means accessing the heap memory (using malloc and free), or in languages like Python it just means the memory managed by the language runtime.

To do access store, we add to the language 4 constructs: new, deref, set, and free. new allocates a fresh location in the store. Think of this as allocating some new memory and putting the result in that location.deref dereferences a given location to return the value stored in that location. set updates the location to store a new value, and free removes a location from the state thus freeing up space. Thus our previous language is now extended to have the following forms:

The state 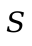is a mapping of locations 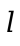to values 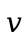. The values in our language now also include locations. These locations are abstract labels that just denotes a place where we can store values. In some languages they are references, in languages like C or C++, they are the direct memory addresses.

The term (seq e1 e2) is simplified to show a sequence of two operations. In practice, our language will support the more general form that supports a sequence of n expressions (seq e1 e2 ... en).

Here is an example of a program using the state:

This program creates a new location to store 5 and binds x to this new location. Following that, it runs a sequence of statements, where it updates the value stored in the location contained in x to 6. Finally, it adds 3 to the updated value. This computation should return 9 as a result. Notice, as x is a reference now, we have to use deref to dereference the value from the location stored in x.

12.3 Modeling the State🔗

We model state as a global store that maps locations to their values. This is a very abstract model of state, but it is one of the most general ways to model it. If you are concerned the environment sounds just like the state, then you are right—they have a lot of similarities, but the biggest one is the state is mutable. Let us demonstrate this through 3 operations we define on the state:

First, update takes a state, a location, and a value and creates a new state such that the provided location has the updated value. If such a location does not exist, it it created in the state.

The get function takes a state and a location and returns the value stored in that location.

Finally, the del function removes location from the state, freeing up storage. Any further accesses to that location will now fail.

12.4 Meaning of State🔗

Now we are ready to give precise meaning of programs that handle state. The global state can change as the program is executing. In other words, as programs were evaluated before they only produced a value, but now evaluation of programs will require an initial state and once evaluated it will yield a final state and the value produced from the computation.

To write this we will change the judgement of our formal rules. Now our judgment will look like E ⊢ ⟨S, e⟩ ⇓ ⟨S, v⟩. This means under a given environment E, our rules take a tuple of the initial state S and expression e and evaluate it the final state S and a value v.

As an example, here is a selection of a few previous rules written to use the state notation:

We add a state to the inference rules to show that it may change whenever any expression is evaluated, and the evolution of the state now gives a notion of ordering in our evaluation. For example, in add, the state starts off with S, but after evaluation of e1, it may evolve to a different state S1. e2 is now evaluated under this state S1 to produce a new state S2, which is the final result of the evaluation of (+ e1 e2). Contrast this with previous rules of addition, it did not matter whether we evaluated e1 or e2 before.

All other rules also incorporate a similar change for state. As an example, the lambda and function application rule is also shown.

Now, we can focus on giving meaning to the newly added parts of the language:

The meaning of (seq e1 e2) is to execute e1 and e2 in sequence. The state evolves through the computation and is used for evaluating e2. The entire block evaluates to the meaning of e2. The rule can be extended for any number of expressions inside seq.

The meaning of (new e) is to allocate a new location in the store, and store the meaning of e in that location. The newly allocated location is the meaning of (new e).

The meaning of (deref e) is to dereference a location in the store, and get the value stored at that location.

The meaning of (set e1 e2) is to get the location to be updated from the meaning of e1 and the value to be updated to from e2 and update the location from e1 to the meaning of e2.

The meaning of (free e) is to delete the location from the meaning of e in the state and mean the deleted location.

Through all these operations the state might change because any subexpression may modify the state. Hence, the state may evolve and it is threaded forward as each of the subexpressions are evaluated.

12.5 Interpreter for a Stateful Language🔗

If you notice carefully, unlike the environment which sends variables out of scope when needed, the state does not do anything like that. The state behaves like a global store, that has locations, once added persist until they are removed. Thus, we can simplify our implementation by moving all the update, get, and del operations by updating the state in-place. We will represent the state in our implementation using a Racket hash table. The function make-hash creates an empty hash table.

For the seq case, which just runs the interp function on all the sub-expressions one by one and the final value is returned. The state S is updated in-place so as long as the evaluation of the subexpression happens in sequence it matches the meaning of (seq e1 e2 ... e3).

For the new case, we define interp-new, we first need a fresh location. We use the Racket provided gensym function for this. It is guaranteed to produce a fresh symbol each time it is called. The subexpression e is evaluated and it is stored in the hash (i.e., our state) with l mapping to the value and the location is returned.

To handle deref, we define interp-deref, where our interpreter evaluates the subexpression and looks up the hash for that location which is then returned.

For handling set, the two subexpressions are evaluated and then the location is updated with the new value from the second subexpression.

Finally, the free function removes the given reference from the state. Any future access to the same location will result in an error.

Putting all these pieces together, the full interpreter looks like below:

state/interp.rkt

#lang racket

(provide interp)

(struct Closure (E e) #:prefab)

(define (store E x v)

(cons (cons x v) E))

(define (lookup E x)

(match E

['() (error "variable not found!")]

[(cons (cons y v) E) (if (eq? x y) v

(lookup E x))]))

(define (interp-div E S e1 e2)

(match* ((only-int (interp E S e1)) (only-int (interp E S e2)))

[(v1 0)  (error "Division by 0 not allowed!")]

[(v1 v2) (quotient v1 v2)]))

(define (only-int v)

(if (integer? v)

v

(error "Integer expected!")))

(define (interp-zero? E S e)

(match (interp E S e)

[0 #t]

[_ #f]))

(define (interp-and E S e1 e2)

(match (interp E S e1)

[#f #f]

[_  (interp E S e2)]))

(define (interp-if E S e1 e2 e3)

(match (interp E S e1)

[#f (interp E S e3)]

[_  (interp E S e2)]))

(define (interp-let E S x e1 e2)

(let* ((v1 (interp E S e1))

(E2 (store E x v1)))

(interp E2 S e2)))

(define (interp-seq E S es)

(match es

[(cons e '()) (interp E S e)]

[(cons e es)  (begin

(interp E S e)

(interp-seq E S es))]))

(define (interp-new E S e)

(let ((v (interp E S e))

(l (gensym)))

(begin

(hash-set! S l v)

l)))

(define (interp-deref E S e)

(let ((l (interp E S e)))

(hash-ref S l)))

(define (interp-set E S e1 e2)

(let ((l (interp E S e1))

(v (interp E S e2)))

(begin

(hash-set! S l v)

v)))

(define (interp-free E S e)

(let ((l (interp E S e)))

(begin0

(hash-remove! S l)

l)))

; Env -> State -> Expr -> Val)

(define (interp E S e)

(match e

[(? integer?)            e]

[(? boolean?)            e]

[(? Closure?)            e]

[(? symbol?)             (lookup E e)]

[`(λ (,x) ,e1)           (Closure E e)]

[`(add1 ,e)              (+ (interp E S e) 1)]

[`(sub1 ,e)              (- (interp E S e) 1)]

[`(zero? ,e)             (interp-zero? E S e)]

[`(+ ,e1 ,e2)            (+ (interp E S e1) (interp E S e2))]

[`(- ,e1 ,e2)            (- (interp E S e1) (interp E S e2))]

[`(* ,e1 ,e2)            (* (interp E S e1) (interp E S e2))]

[`(/ ,e1 ,e2)            (interp-div E S e1 e2)]

[`(<= ,e1 ,e2)           (<= (only-int (interp E S e1)) (only-int (interp E S e2)))]

[`(and ,e1 ,e2)          (interp-and E S e1 e2)]

[`(if ,e1 ,e2 ,e3)       (interp-if E S e1 e2 e3)]

[`(let ((,x ,e1)) ,e2)   (interp-let E S x e1 e2)]

[`(new ,e)               (interp-new E S e)]

[`(deref ,e)             (interp-deref E S e)]

[`(set ,e1 ,e2)          (interp-set E S e1 e2)]

[`(free ,e)              (interp-free E S e)]

[`(seq ,@es)             (interp-seq E S es)]

[`(,e1 ,e2)              (match (interp E S e1)

[(Closure E1 `(λ (,x) ,e3)) (interp (store E1 x (interp E S e2)) S e3)]

[_            (error "Cannot apply non-function!")])]

[_                       (error "Parser error!")]))

Running the interpreter now requires an empty environment and an empty state, so we can write a convenience function, eval, that instantiates these and calls the interp function.

12.6 Testing🔗

We can write a few tests to check if the interpreter is behaving as we would expect:

Previously, in Lambda: First-class Functions, we used the Y-combinator with call-by-name to write recursive functions, but now we can do it more naturally.

These can be written down as test cases:

12.7 Aliasing and Mutability🔗

TODO