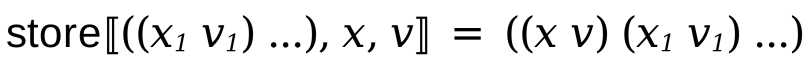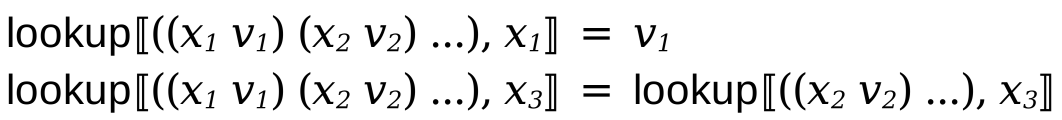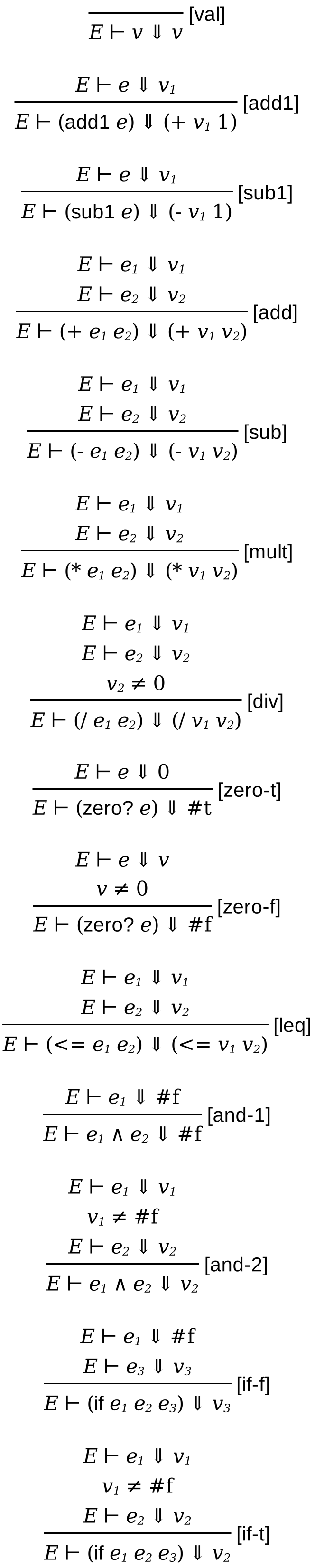10 Environments🔗

10.1 Problems with Substitution🔗

We have a working language with variables, let bindings, and lambdas. Most of your programming experience has taught you that when a language encounters an identifier, it has to “look it up”. Not only does our interpreter not look up anything, we defined its behavior on variables to be an error! While absolutely correct, this is also a little surprising. More importantly, we write interpreters to understand and explain languages, and this implementation might strike you as not doing that, because it doesn’t match our intuition.

Moreover, if you think about how you use lambdas or functions in a common language (like JavaScript or Python), it can use variables that were available to the function at the time of definition, even outside it’s scope. The key contribution of alpha-reduction is to rename such captured variables uniquely such that you get the same behavior as mainstream languages: ability to use variables that were available at the time of function definition.

In the example above, the function fn captures the value of x as 2 and whenever it is applied, the function body gets the value x as 2. You might know this behavior as closure. Substitution gave us the same behavior as a closure without constructing one, but it does not fit our mental model of languages.

There’s another problem with substitution, which is the number of times it has traverse the source program. It would be nice to have to traverse only those parts of the program that are actually evaluated and only when necessary. But substitution traverses everything, like unvisited branches of conditionals, and forces the program to be traversed once for substitution and once again for interpretation.

In this module, we will migrate to a model of how real languages are implemented that matches closely with our mental model of variables and closures.

10.2 Syntax🔗

Below is the same syntax we had for our language, but with a few differences:

First, notice E in the language? That is the environment. It is a mapping of variables to values stored as a sequence. This fits our mental model: when we declare variables we store them in the environment and when we evaluate variables we look up their values the environment. This also addresses our second concern about traversing the source program too many times. Storing a variable in the environment merely denotes our intent to substitute the identifier later on. Only when we evaluate a variable do we substitute it by looking up in the environment. In practice, all commonly used languages use the environment in their implementation.

Second, notice the new value Closure? It is a tuple that contains an environment and an expression. Because lambdas capture the variables declared before it, we need to store both the environment and the lambda itself in the closure. Crucially, the lambda expression (λ (x) e) is not a value anymore, it has moved to being an expression that has to be evaluated to yield a closure. Everything else in the language syntax stays the same.

10.3 Environments🔗

We already saw that environments are a mapping of variables to values. Now, to support storing variable and the values they are bound to and lookups we have two define two operations on our environment.

First, we define store as a function that given an environment, a variable, and a value to be stored, it adds it to the environment and returns this new environment.

Similarly, we will define a function lookup that given an environment and a variable looks up the the environment and returns the value bound to that variable.

The lookup function, if it finds the variable it is looking for returns the value bound to it. Otherwise, it recurses and continues the lookup in the remainder of the environment.

Notice, how the new environment stores the variable binding in the front of the sequence and how the lookup starts the lookup from the start of that sequence? This enables the store and lookup to find the most recently bound value of a variable in a program.

The program above returns the value 3 which is the most recent value bound to x and our lookup and store functions work in conjunction to find the most recent binding.

10.4 Semantics with Environments🔗

With the addition of an environment, the semantics of our language changes slightly, as shown below. However, this does not change the meaning for most of the language. The E ⊢ is now a part of all rules in our language. The ⊢ symbol is called the turnstile. In this context, you can read this as: given an environment E, (+ e1 e2) means (+ v1 v2) if e1 means v1 in the same environment E and e2 means v2 under the same environment E.

The rules are more interesting for rest of the language that actually deal with looking up or binding new variables.

Unlike substitution, where variables did not have an semantics because they were substituted away, variables with an environment are looked up in the environment they are evaluated under. The var rules specifies this.

Expressions like (λ (x) e) are evaluated to a Closure by capturing the environment it is evaluated with and the lambda expression itself. This is how closures remember the variables bound before it.

let bindings evaluate the binding expression e1 and store it in the given environment with the identifier x mapping to the resulting value. This new environment is used to evaluate the body of the let binding e2 which gives the resulting meaning of the full let binding.

Function applications are defined in the app rule. The function position expression e1 has to evaluate to a closure for it to be applied to another expression e2. Finally, the body of the lambda stored in the closure is evaluated with the environment stored in the closure, with additional bindings of the argument of the lambda (x) bound to the argument of the function application (v2).

Note, how these changes do not change the language from the perspective of the user. The user can write the same programs as they wrote in Lambda: First-class Functions. All we are changing is the implementation strategy. We can now write an interpreter that uses environments.

10.5 Interpreter with Environments🔗

We will use Racket’s lists to define our environment. One could use Racket’s hash tables to implement environments as well.

For our implementation, an empty environment is '(). Storing a variable to a value stores a pair in the environment. So an environment containing x = 2 will be denoted as '((x . 2)). Storing y = 5 in the same environment, will result in a new environment '((y . 5) (x . 2)). The same variables can be redefined as well. If we re-bind x = 42 in the environment, it will be stored as '((x . 42) (y . 5) (x . 2)). We define a function store to define this operation:

Similarly, our look up operation on the environment will walk the list and return the first occurrence of the identifier. If it is not found it will raise an error:

Notice how the variable not found in our interpreter moved to the lookup function above?

We define Closure as a Racket struct that stores the environment and the expression. This is how the final interpreter looks:

environments/interp.rkt

#lang racket

(provide interp)

(struct Closure (E e) #:prefab)

(define (store E x v)

(cons (cons x v) E))

(define (lookup E x)

(match E

['() (error "variable not found!")]

[(cons (cons y v) E) (if (eq? x y) v

(lookup E x))]))

(define (interp-div E e1 e2)

(match* ((only-int (interp E e1)) (only-int (interp E e2)))

[(v1 0)  (error "Division by 0 not allowed!")]

[(v1 v2) (quotient v1 v2)]))

(define (only-int v)

(if (integer? v)

v

(error "Integer expected!")))

(define (interp-zero? E e)

(match (interp E e)

[0 #t]

[_ #f]))

(define (interp-and E e1 e2)

(match (interp E e1)

[#f #f]

[_  (interp E e2)]))

(define (interp-if E e1 e2 e3)

(match (interp E e1)

[#f (interp E e3)]

[_  (interp E e2)]))

(define (interp-let E x e1 e2)

(let* ((v1 (interp E e1))

(E2 (store E x v1)))

(interp E2 e2)))

; Env -> Expr -> Val

(define (interp E e)

(match e

[(? integer?)            e]

[(? boolean?)            e]

[(? symbol?)             (lookup E e)]

[`(λ (,x) ,e1)           (Closure E e)]

[`(add1 ,e)              (+ (interp E e) 1)]

[`(sub1 ,e)              (- (interp E e) 1)]

[`(zero? ,e)             (interp-zero? E e)]

[`(+ ,e1 ,e2)            (+ (interp E e1) (interp E e2))]

[`(- ,e1 ,e2)            (- (interp E e1) (interp E e2))]

[`(* ,e1 ,e2)            (* (interp E e1) (interp E e2))]

[`(/ ,e1 ,e2)            (interp-div E e1 e2)]

[`(<= ,e1 ,e2)           (<= (only-int (interp E e1)) (only-int (interp E e2)))]

[`(and ,e1 ,e2)          (interp-and E e1 e2)]

[`(if ,e1 ,e2 ,e3)       (interp-if E e1 e2 e3)]

[`(let ((,x ,e1)) ,e2)   (interp-let E x e1 e2)]

[`(,e1 ,e2)              (match (interp E e1)

[(Closure E1 `(λ (,x) ,e3)) (interp (store E1 x (interp E e2)) e3)]

[_            (error "Cannot apply non-function!")])]

[_                       (error "Parser error!")]))

All functions related to substitution (free?, alpha-reduce, and beta-reduce) are gone! The cases in the interp function are updated to call the store and lookup functions and use Closure. Just like how our inference rules were updated when we defined the meaning of the language to include an environment, our interp and similar functions are also updated to include the environment E as a parameter.

Running our interpreter now requires us to pass the environment. We just pass an empty environment '() to it. The interpreter produce results as expected. The last example, in particular, demonstrates how a closure captures the environment (x = 3 in this case) to be used when the function is called later.

10.6 Testing🔗

We can convert these to a test cases that can checked automatically:

10.7 Why Substitution?🔗

If substitutions and environments result in the same thing, why did we take the long winded way to learn both?

Substitutions take an expression-centric view on bindings, i.e., all operations are done at the expression level. Environments, on the other hand, take an abstract machine view of bindings: there is some environment in any machine that you can store or do lookup in while interpreting you program.

The former might be tedious to implement but is useful when checking certain programs for equivalence or doing proofs because all we have to compare is the expression and nothing else. The latter provides an easier and faster implementation in practice when building language interpreters.

Having two ways to realize the same thing is great as we can cross-check our implementation against both to see if they agree. If they do not, at least one of them is wrong. We can also prove that both approaches will give the same result for all possible programs in our language, but that is out of scope for this class. But as an exercise you could compare your two interpreters by checking if they agree on multiple programs:

check-equal? (interp-subst e) (interp-env '() e)

where e is some expression in our language. You will have to write some additional code to correctly compare closures and lambda terms returned by the substitution based interpreter. You could through a random set of programs at this checker to build confidence that both are interpreters are indeed equivalent.